Posted on | In

This blog refers to this paper

Abstract

We propose a method for semi-supervised semantic segmentation using the adversarial network. While most existing discriminators are trained to classify input images as real or fake on the image level, we design a discriminator in a fully convolutional manner to differentiate the predicted probability maps from the ground truth segmentation distribution with the consideration of the spatial resolution. We show that the proposed discriminator can be used to improve the performance on semantic segmentation by coupling the adversarial loss with the standard cross entropy loss on the segmentation network. In addition, the fully convolutional discriminator enables the semi-supervised learning through discovering the trustworthy regions in prediction results of unlabeled images, providing additional supervisory signals. In contrast to existing methods that utilize weakly-labeled images, our method leverages unlabeled images without any annotation to enhance the segmentation model. Experimental results on both the PASCAL VOC 2012 dataset and the Cityscapes dataset demonstrate the effectiveness of our algorithm.

Architecture and training pipeline

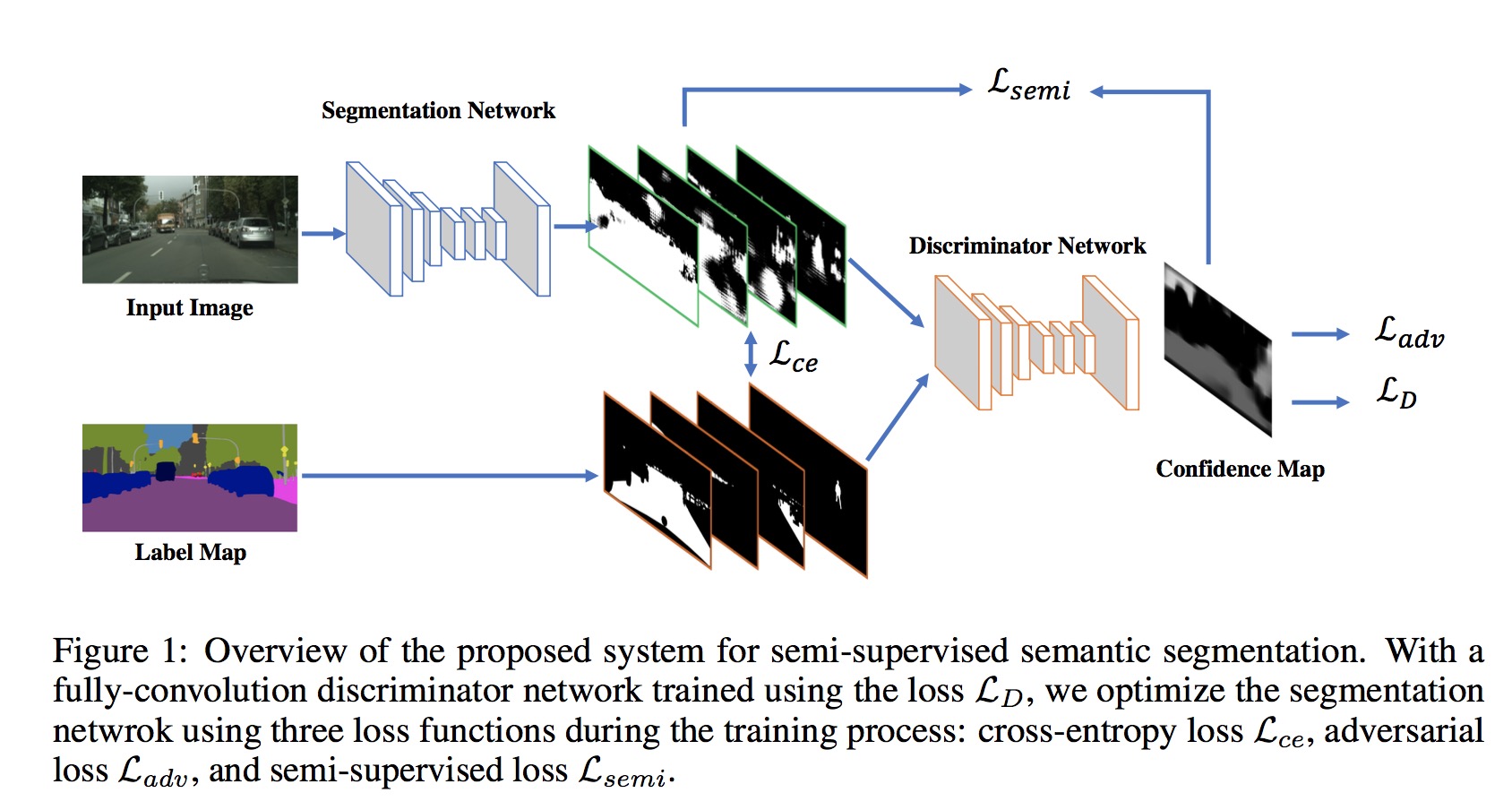
The authors firstly train the segmentation network with cross-entropy loss and adversarial loss and the discriminitor network with cross-entropy loss in labeled data. Then, the training of unlabeled data is performed under the semi-cross-entropy loss with the self-taught ground truth from the trained discriminitor network and threshold settings.

Discriminator network training

$L_D = -\sum_{h, w} (1-y_n)log(1-D(S(X_n)^{h, w})) + y_n D(Y_n)^{h, w}$

$X_n$ is the input image, whose size is H x W x 3. S() is the segmentation network, whose input is $X_n$ and output is H x W x C probability maps. And D() is discriminator network, which takes H x W x C probability maps and predict the probabilities for each pix from segmentaiton network or groundtruth. Thus, the cross-entropy loss is binary cross-entropy, where $y_n = 0$ if the sample is drawn from segmentation network and $y_n = 1$ if the sample is from ground truth label.

Segmentation network training

$L_{seg} = L_{ce} + \lambda_{adv} L_{adv} + \lambda_{semi} L_{semi}$

where $L_{seg}, L_{ce}$ and $L_{adv}$ denote multi-class cross-entropy loss, adversarial loss and semi-supervised loss, respectively, $\lambda_{adv}$ and $\lambda_{semi}$ are two constants for balancing the multi-task training.

Training with labeled data

$L_{ce} = -\sum_{h, w} Y_n^{(h, w, c)}log(S(X_n)^{(h, w, c)})$
, where $Y_n$ is one-hot encoded ground truth, and $S(X_n)$ is the prediction probability maps.

$L_{adv} = -\sum_{h, w} log(D(S(X_n))^{h, w})$
with this adversarial loss, we seek to train the segmentation network to fool the discriminator by maximizing the probability of the segmentation prediction being considered as the ground truth distribution.

In fact, you can regard $D(S(X_n))$ as $D(S(X_n)) = P(y_n=1|S(X_n))$, which means the probability where sample are drawn from segmentation network but the discriminator assume it’s from ground-truth.

Training with un-labeled data

$L_{semi} = -\sum_{h,w}\sum_{c \in C}I(D(S(X_n)^{h,w} > T_{semi}) \hat{Y}_n^{(h,w,c)}log(S(X_n)_{(h,w,c)})$

where, $\hat{Y_n} = argmax(S(X_n))$ the masked segmentation prediction, $T_{semi}$ is threshold to control the sensitivity of the self-taught process, since there’s no ground-truth for $L_{ce}$.

Posted on | In

cited from 莫烦python

np.vstack()

对于一个array的合并，我们可以想到按行、按列等多种方式进行合并。首先先看一个例子：

1
2
3
4
5
6
7
8
9
import numpy as np
A = np.array([1,1,1])
B = np.array([2,2,2])
         
print(np.vstack((A,B)))    # vertical stack
"""
[[1,1,1]
 [2,2,2]]
"""

vertical stack本身属于一种上下合并，即对括号中的两个整体进行对应操作。此时我们对组合而成的矩阵进行属性探究：

1
2
3
4
C = np.vstack((A,B))      
print(A.shape,C.shape)

# (3,) (2,3)

np.hstack()

利用shape函数可以让我们很容易地知道A和C的属性，从打印出的结果来看，A仅仅是一个拥有3项元素的数组（数列），而合并后得到的C是一个2行3列的矩阵。

介绍完了上下合并，我们来说说左右合并：

1
2
3
4
5
6
7
D = np.hstack((A,B))       # horizontal stack

print(D)
# [1,1,1,2,2,2]

print(A.shape,D.shape)
# (3,) (6,)

通过打印出的结果可以看出：D本身来源于A，B两个数列的左右合并，而且新生成的D本身也是一个含有6项元素的序列。

np.newaxis()

说完了array的合并，我们稍稍提及一下前一节中转置操作，如果面对如同前文所述的A序列， 转置操作便很有可能无法对其进行转置（因为A并不是矩阵的属性），此时就需要我们借助其他的函数操作进行转置：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
print(A[np.newaxis,:])
# [[1 1 1]]

print(A[np.newaxis,:].shape)
# (1,3)

print(A[:,np.newaxis])
"""
[[1]
[1]
[1]]
"""

print(A[:,np.newaxis].shape)
# (3,1)

此时我们便将具有3个元素的array转换为了1行3列以及3行1列的矩阵了。

结合着上面的知识，我们把它综合起来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
A = np.array([1,1,1])[:,np.newaxis]
B = np.array([2,2,2])[:,np.newaxis]
         
C = np.vstack((A,B))   # vertical stack
D = np.hstack((A,B))   # horizontal stack

print(D)
"""
[[1 2]
[1 2]
[1 2]]
"""

print(A.shape,D.shape)
# (3,1) (3,2)

np.concatenate()

当你的合并操作需要针对多个矩阵或序列时，借助concatenate函数可能会让你使用起来比前述的函数更加方便：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
C = np.concatenate((A,B,B,A),axis=0)

print(C)
"""
array([[1],
       [1],
       [1],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [1],
       [1],
       [1]])
"""

D = np.concatenate((A,B,B,A),axis=1)

print(D)
"""
array([[1, 2, 2, 1],
       [1, 2, 2, 1],
       [1, 2, 2, 1]])
"""

axis参数很好的控制了矩阵的纵向或是横向打印，相比较vstack和hstack函数显得更加方便。

Posted on | In

377. Combination Sum IV

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.

Example:

nums = [1, 2, 3]
target = 4

The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

Note that different sequences are counted as different combinations.

Therefore the output is 7.
Follow up:
What if negative numbers are allowed in the given array?
How does it change the problem?
What limitation we need to add to the question to allow negative numbers?

Idea

dp or memorized dfs: they are same in fact.

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution(object):
    def combinationSum4(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
#         memory = {}
#         nums.sort()
        
#         def dfs(target):
#             if target in memory:
#                 return memory[target]
            
#             res = 0
#             for num in nums:
#                 if num > target:
#                     break
#                 elif num == target:
#                     res += 1
#                 else:
#                     res += dfs(target - num)
#             memory[target] = res
#             return res       
#         return dfs(target)
        nums.sort()
        dp = [0] * (target + 1)
        dp[0] = 1 # if num == target
        for t in range(1, target + 1):
            for n in nums:
                if n > t:
                    break
                dp[t] += dp[t - n]
        print dp
        return dp[target]

Posted on | In

721. Accounts Merge

Given a list accounts, each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account.

Now, we would like to merge these accounts. Two accounts definitely belong to the same person if there is some email that is common to both accounts. Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name.

After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order.

Example 1:

1
2
3
4
5
6
7
8
Input: 
accounts = [["John", "johnsmith@mail.com", "john00@mail.com"], ["John", "johnnybravo@mail.com"], ["John", "johnsmith@mail.com", "john_newyork@mail.com"], ["Mary", "mary@mail.com"]]
Output: [["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'],  ["John", "johnnybravo@mail.com"], ["Mary", "mary@mail.com"]]
Explanation: 
The first and third John's are the same person as they have the common email "johnsmith@mail.com".
The second John and Mary are different people as none of their email addresses are used by other accounts.
We could return these lists in any order, for example the answer [['Mary', 'mary@mail.com'], ['John', 'johnnybravo@mail.com'], 
['John', 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com']] would still be accepted.

Note:

The length of accounts will be in the range [1, 1000].
The length of accounts[i] will be in the range [1, 10].
The length of accounts[i][j] will be in the range [1, 30].

Idea

Union-find the emails. The emails in an account belong to one group. Since, we can not directly perform uf operations on the strs, so we need mapping them between int array.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class UnionFind(object):
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.rank = [0] * n
        
    def union(self, n, m):
        p, q = self.find(n), self.find(m)
        if p != q:
            if self.rank[p] > self.rank[q]:
                self.parent[q] = p
            else:
                self.parent[p] = q
                if self.rank[p] == self.rank[q]:
                    self.rank[q] += 1
        
    def find(self, n):
        if self.parent[n] != n:
            return self.find(self.parent[n])
        return n

class Solution(object):
    def accountsMerge(self, accounts):
        """
        :type accounts: List[List[str]]
        :rtype: List[List[str]]
        """
        # init
        eid = 0     # email id
        e2n = {}    # email to name
        e2i = {}    # email to email id
        i2e = {}    # email id to email
        for account in accounts:
            name = account[0]
            for email in account[1:]:
                if not (email in e2i):
                    e2n[email] = name
                    e2i[email] = eid
                    i2e[eid] = email
                    eid += 1

        # union find
        uf = UnionFind(eid + 1)
        for account in accounts:
            first_eid = e2i[account[1]]
            for email in account[2:]:
                uf.union(first_eid, e2i[email])
        
        # prev steps to construct answer:
        # find the all the parent emails as well as their children in a group
        p2c = collections.defaultdict(set)    # parent email to children emails
        for account in accounts:
            for email in account[1:]:
                parent_email_id = uf.find(e2i[email])
                parent_email = i2e[parent_email_id]
                p2c[parent_email].add(email)
        
        # construct the answers
        res = []
        for parent in p2c:
            tmp = []
            name = e2n[parent]
            tmp = [name]
            tmp += sorted(list(p2c[parent]))
            res.append(tmp)
            
        return res

Posted on | In

98. Validate Binary Search Tree

Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.
Example 1:

1
2
3
4
5
Input:
    2
   / \
  1   3
Output: true

Example 2:

1
2
3
4
5
6
    5
   / \
  1   4
     / \
    3   6
Output: false

Explanation: The input is: [5,1,4,null,null,3,6]. The root node’s value
is 5 but its right child’s value is 4.

Idea

Recurison inorderly. Or divide and conquer.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution(object):
    def isValidBST(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        self.order = []
        self.inorder(root)
        
        prev = float('-inf')
        for node in self.order:
            if node.val <= prev:
                return False
            prev = node.val
        
        return True

    def inorder(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if root is None:
            return
        
        self.inorder(root.left)
        self.order.append(root)
        self.inorder(root.right)

# version 2
# class Solution(object):
#     def isValidBST(self, root):
#         """
#         :type root: TreeNode
#         :rtype: bool
#         """
#         res, _, _ = self.helper(root)
#         return res

#     def helper(self, root):
#         """
#         :type root: TreeNode
#         :rtype: bool
#         """
#         if root is None:
#             return True, float('-inf'), float('inf')
#         left, leftmax, leftmin = self.helper(root.left)
#         right, rightmax, rightmin = self.helper(root.right)

#         rootmax = max(root.val, max(leftmax, rightmax))
#         rootmin = min(root.val, min(rightmin, leftmin))
        
#         if left and right:
#             return leftmax < root.val and root.val < rightmin, rootmax, rootmin 

#         return False, float('-inf'), float('inf')

Posted on | In

786. K-th Smallest Prime Fraction

A sorted list A contains 1, plus some number of primes. Then, for every p < q in the list, we consider the fraction p/q.

What is the K-th smallest fraction considered? Return your answer as an array of ints, where answer[0] = p and answer[1] = q.

Examples:
Input: A = [1, 2, 3, 5], K = 3
Output: [2, 5]
Explanation:
The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, 2/3.
The third fraction is 2/5.

Input: A = [1, 7], K = 1
Output: [1, 7]

Idea

Binary Search + Matrix
cited from 花花酱

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution(object):
    def kthSmallestPrimeFraction(self, A, K):
        """
        :type A: List[int]
        :type K: int
        :rtype: List[int]
        """
        l = 0.0
        r = 1.0
        n = len(A)
        while l < r:
            m = l + (r - l) / 2
            max_f = 0.0
            tot = 0
            p, q = 0, 0
            j = 1
            for i in range(0, n - 1):
                while j < n and A[i] > m * A[j]: # find the first ele in a row smaller than m
                    j += 1
                tot += n - j # add the number of elements smaller than m in this row
                if n == j: # no ele smaller than m
                    break
                f = 1.0 * A[i] / A[j]
                if f > max_f: # find the largest frac in the k fracs
                    p, q, max_f = i, j , f
            if tot == K:
                return [A[p], A[q]]
            elif tot > K: # m too large
                r = m
            else:         # m too small
                l = m
        return []

Posted on | In

636. Exclusive Time of Functions

Given the running logs of n functions that are executed in a nonpreemptive single threaded CPU, find the exclusive time of these functions.

Each function has a unique id, start from 0 to n-1. A function may be called recursively or by another function.

A log is a string has this format : function_id:start_or_end:timestamp. For example, “0:start:0” means function 0 starts from the very beginning of time 0. “0:end:0” means function 0 ends to the very end of time 0.

Exclusive time of a function is defined as the time spent within this function, the time spent by calling other functions should not be considered as this function’s exclusive time. You should return the exclusive time of each function sorted by their function id.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input:
n = 2
logs = 
["0:start:0",
 "1:start:2",
 "1:end:5",
 "0:end:6"]
Output:[3, 4]
Explanation:
Function 0 starts at time 0, then it executes 2 units of time and reaches the end of time 1. 
Now function 0 calls function 1, function 1 starts at time 2, executes 4 units of time and end at time 5.
Function 0 is running again at time 6, and also end at the time 6, thus executes 1 unit of time. 
So function 0 totally execute 2 + 1 = 3 units of time, and function 1 totally execute 4 units of time.

Idea

This is a simulation. The scenario can easily bring the stack into our mind, since the real-process of threads is through stack. The stack may hold the tid.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution(object):
    def exclusiveTime(self, n, logs):
        """
        :type n: int
        :type logs: List[str]
        :rtype: List[int]
        """
        ans = [0] * n
        stack = []
        
        prev = 0
        for log in logs:
            fid, command, time = log.split(":")
            fid, time = int(fid), int(time)
            
            if command == 'start':
                if stack:
                    ans[stack[-1]] += time - prev
                stack.append(fid)
                prev = time
            else:
                ans[stack.pop()] += time - prev + 1 # draw a picture and run a case, this part can be finished
                prev = time + 1
                
        return ans

Posted on | In

670. Maximum Swap

Given a non-negative integer, you could swap two digits at most once to get the maximum valued number. Return the maximum valued number you could get.

Example 1:

1
2
3
Input: 2736
Output: 7236
Explanation: Swap the number 2 and the number 7.

Example 2:

1
2
3
Input: 9973
Output: 9973
Explanation: No swap.

Note:
The given number is in the range [0, 10^8]

Idea

Simply thinking, brute force is ok, whose time complexity is O(n^2). In fact, for the former bit, we should find a largest bit which occurs latest, which is the solution.

1
2
largest 7689 >> 9687
latest 7688 >> 8687

Code

cited from https://leetcode.com/problems/maximum-swap/discuss/107066/Python-Straightforward-with-Explanation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def maximumSwap(self, num):
        """
        :type num: int
        :rtype: int
        """
        A = map(int, str(num))
        num2idx = {x: i for i, x in enumerate(A)}
        for i, x in enumerate(A):
            for larger in range(9, x, -1):
                if num2idx.get(larger, -1) > i: # find a larger bit which is later
                    A[i], A[num2idx[larger]] = A[num2idx[larger]], A[i]
                    return int("".join(map(str, A)))
        return num

Thinking

How about 9973, where ‘num2idx = {x: i for i, x in enumerate(A)}’ may omits 9:0 pair and leave 9:1 ?

Python

map(function, iterable, …)

1
2
3
4
5
6
7
8
9
10
11
>>>def square(x) :            # 计算平方数
...     return x ** 2
... 
>>> map(square, [1,2,3,4,5])   # 计算列表各个元素的平方
[1, 4, 9, 16, 25]
>>> map(lambda x: x ** 2, [1, 2, 3, 4, 5])  # 使用 lambda 匿名函数
[1, 4, 9, 16, 25]
 
# 提供了两个列表，对相同位置的列表数据进行相加
>>> map(lambda x, y: x + y, [1, 3, 5, 7, 9], [2, 4, 6, 8, 10])
[3, 7, 11, 15, 19]

map(int, str(123))

1
2
>> map(int, ['1', '2', '3'])
>> map([int('1'), int('2'), int('3')])

Posted on | In

215. Kth Largest Element in an Array

Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Example 1:

Input: [3,2,1,5,6,4] and k = 2
Output: 5
Example 2:

Input: [3,2,3,1,2,4,5,5,6] and k = 4
Output: 4

Idea

heap

Code

1
2
3
4
5
6
7
8
class Solution(object):
    def findKthLargest(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        return list(heapq.nlargest(k,nums))[-1]

python中的堆排序peapq模块

cited from: https://github.com/qiwsir/algorithm/blob/master/heapq.md
heapq模块实现了python中的堆排序，并提供了有关方法。让用Python实现排序算法有了简单快捷的方式。

heapq的官方文档和源码：8.4.heapq-Heap queue algorithm

下面通过举例的方式说明heapq的应用方法

##实现堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
#! /usr/bin/evn python
#coding:utf-8

from heapq import *

def heapsort(iterable):
    h = []
    for value in iterable:
        heappush(h,value)
    return [heappop(h) for i in range(len(h))]

if __name__=="__main__":
    print heapsort([1,3,5,9,2])

###heappush()

heapq.heappush(heap, item):将item压入到堆数组heap中。如果不进行此步操作，后面的heappop()失效

###heappop()

heapq.heappop(heap):从堆数组heap中取出最小的值，并返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
>>> h=[]                    #定义一个list
>>> from heapq import *     #引入heapq模块
>>> h
[]
>>> heappush(h,5)               #向堆中依次增加数值
>>> heappush(h,2)
>>> heappush(h,3)
>>> heappush(h,9)
>>> h                           #h的值
[2, 5, 3, 9]
>>> heappop(h)                  #从h中删除最小的，并返回该值
2
>>> h
[3, 5, 9]
>>> h.append(1)                 #注意，如果不是压入堆中，而是通过append追加一个数值
>>> h                           #堆的函数并不能操作这个增加的数值，或者说它堆对来讲是不存在的
[3, 5, 9, 1]
>>> heappop(h)                  #从h中能够找到的最小值是3,而不是1
3
>>> heappush(h,2)               #这时，不仅将2压入到堆内，而且1也进入了堆。
>>> h
[1, 2, 9, 5]
>>> heappop(h)                  #操作对象已经包含了1
1

###heapq.heappushpop(heap, item)

是上述heappush和heappop的合体，同时完成两者的功能.注意：相当于先操作了heappush(heap,item),然后操作heappop(heap)

1
2
3
4
5
6
7
8
>>> h
[1, 2, 9, 5]
>>> heappop(h)
1
>>> heappushpop(h,4)            #增加4同时删除最小值2并返回该最小值，与下列操作等同：
2                               #heappush(h,4),heappop(h)
>>> h
[4, 5, 9]

###heapq.heapify(x)

x必须是list，此函数将list变成堆，实时操作。从而能够在任何情况下使用堆的函数。

1
2
3
4
5
6
7
8
9
10
>>> a=[3,6,1]
>>> heapify(a)                  #将a变成堆之后，可以对其操作
>>> heappop(a)
1
>>> b=[4,2,5]                   #b不是堆，如果对其进行操作，显示结果如下
>>> heappop(b)                  #按照顺序，删除第一个数值并返回,不会从中挑选出最小的
4
>>> heapify(b)                  #变成堆之后，再操作
>>> heappop(b)
2

###heapq.heapreplace(heap, item)

是heappop(heap)和heappush(heap,item)的联合操作。注意，与heappushpop(heap,item)的区别在于，顺序不同，这里是先进行删除，后压入堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
>>> a=[]
>>> heapreplace(a,3)            #如果list空，则报错
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
IndexError: index out of range
>>> heappush(a,3)
>>> a
[3]
>>> heapreplace(a,2)            #先执行删除（heappop(a)->3),再执行加入（heappush(a,2))
3
>>> a
[2]
>>> heappush(a,5)  
>>> heappush(a,9)
>>> heappush(a,4)
>>> a
[2, 4, 9, 5]
>>> heapreplace(a,6)            #先从堆a中找出最小值并返回，然后加入6
2
>>> a
[4, 5, 9, 6]
>>> heapreplace(a,1)            #1是后来加入的，在1加入之前，a中的最小值是4
4
>>> a
[1, 5, 9, 6]

###heapq.merge(*iterables)

举例：

1
2
3
4
5
>>> a=[2,4,6]         
>>> b=[1,3,5]
>>> c=merge(a,b)
>>> list(c)
[1, 2, 3, 4, 5, 6]

在归并排序中详细演示了本函数的使用方法。

###heapq.nlargest(n, iterable[, key]),heapq.nsmallest(n, iterable[, key])

获取列表中最大、最小的几个值。

1
2
3
4
>>> a   
[2, 4, 6]
>>> nlargest(2,a)
[6, 4]

Posted on | In

133. Clone Graph

Clone an undirected graph. Each node in the graph contains a label and a list of its neighbors.

OJ’s undirected graph serialization:
Nodes are labeled uniquely.

We use # as a separator for each node, and , as a separator for node label and each neighbor of the node.
As an example, consider the serialized graph {0,1,2#1,2#2,2}.

The graph has a total of three nodes, and therefore contains three parts as separated by #.

First node is labeled as 0. Connect node 0 to both nodes 1 and 2.
Second node is labeled as 1. Connect node 1 to node 2.
Third node is labeled as 2. Connect node 2 to node 2 (itself), thus forming a self-cycle.
Visually, the graph looks like the following:

1
2
3
4
5
6
   1
  / \
 /   \
0 --- 2
     / \
     \_/

Idea

Perform bfs algorithm to traverse the whole graph and get all the nodes firstly, and then copy the nodes and construct the mapping from original nodes to new nodes. Finally, copy the edges (neighbors) via the mapping.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    # @param node, a undirected graph node
    # @return a undirected graph node
    def cloneGraph(self, node):
        root = node
        if node is None:
            return None
        
        # bfs traverse the graph
        nodes = self.getNodes(root)
        
        # copy the nodes
        map = {}
        for node in nodes:
            map[node] = UndirectedGraphNode(node.label)
        
        # copy the edges
        for node in nodes:
            for n in node.neighbors:
                map[node].neighbors.append(map[n])
                
        return map[root]
        
        
    def getNodes(self, node):
        que = [node]
        visited = set()
        visited.add(node)
        while que:
            h = que.pop(0)
            for n in h.neighbors:
                if not (n in visited):
                    que.append(n)
                    visited.add(n)
        return list(visited)