Posted on | In

Authors

Andrew G. Howard Menglong Zhu Bo Chen Dmitry Kalenichenko Weijun Wang Tobias Weyand Marco Andreetto Hartwig Adam
Google Inc.
{howarda,menglong,bochen,dkalenichenko,weijunw,weyand,anm,hadam}@google.com

Abstract

We present a class of efficient models called MobileNets for mobile and embedded vision applications. MobileNets are based on a streamlined architecture that uses depth- wise separable convolutions to build light weight deep neural networks. We introduce two simple global hyperparameters that efficiently trade off between latency and accuracy. These hyper-parameters allow the model builder to choose the right sized model for their application based on the constraints of the problem. We present extensive experiments on resource and accuracy tradeoffs and show strong performance compared to other popular models on ImageNet classification. We then demonstrate the effectiveness of MobileNets across a wide range of applications and use cases including object detection, finegrain classifica- tion, face attributes and large scale geo-localization.

Posted on | In

surrounded regions

  • idea:
    start from the edges

  • code:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    vector<vector<char>> board = {{'x', 'x', 'x', 'x'}, {'x', 'o', 'o', 'x'}, {'o', 'x', 'x', 'x'}, {'x', 'o', 'o', 'x'}};
    int row = board.size();
    int col = board[0].size();

    for (int r = 0; r < row; r++) {
        bfs(board, r, 0);
        bfs(board, r, col - 1);
    }

    for (int c = 0; c < col; c++) {
        bfs(board, 0, c);
        bfs(board, row - 1, c);
    }

    for (int r = 0; r < row; r++) {
        for (int c = 0; c < col; c++) {
            if (board[r][c] == 'w') {
                board[r][c] = 'o';
            }
            if (board[r][c] == 'o') {
                board[r][c] = 'w';
            }
        }
    }

    void bfs(vector<vector<char>>& board, int start_r, int start_c) {
        int row = board.size();
        int col = board[0].size();
        vector<pair<int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        queue<pair<int>> que({start_r, start_c});
        for (auto& dir : dirs) {
            int new_r = dir.first + start_r;
            int new_c = dir.second + start_c;

        }
    }

200 Number of Islands

Given a 2d grid map of ‘1’s (land) and ‘0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Example 1:

Input:
11110
11010
11000
00000

Output: 1
Example 2:

Input:
11000
11000
00100
00011

Output: 3

  • idea
    bfs

  • code

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    class Solution(object):
        def numIslands(self, grid):
            """
            :type grid: List[List[str]]
            :rtype: int
            """
            if not grid or len(grid) == 0:
                return 0
            
            self.grid = grid
            self.n, self.m = len(grid), len(grid[0])
            self.visited = [[False] * self.m for _ in range(self.n)]
            
            ans = 0
            for i in range(self.n):
                for j in range(self.m):
                    if grid[i][j] == '1' and not self.visited[i][j]:
                        ans += 1
                        self.visited[i][j] = True
                        self.bfs(i, j)
            return ans
        
        def bfs(self, x, y):
            dzs = zip([1, 0, -1, 0], [0, 1, 0, -1])
            que = [(x, y)]
            while que:
                h = que.pop(0)
                for dz in dzs:
                    x_, y_ = h[0] + dz[0], h[1] + dz[1]
                    if self.isValid(x_, y_) and not self.visited[x_][y_]:
                        self.visited[x_][y_] = True
                        que.append((x_, y_))
                        
        def isValid(self, x, y):
            if x >= 0 and x <= self.n - 1 and \
                y >= 0 and y <= self.m - 1 and \
                self.grid[x][y] == '1':
                    return True
            return False

695. Max Area of Island

Given a non-empty 2D array grid of 0’s and 1’s, an island is a group of 1’s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

Find the maximum area of an island in the given 2D array. (If there is no island, the maximum area is 0.)

Example 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Given the above grid, return 6. Note the answer is not 11, because the island must be connected 4-directionally.
Example 2:
[[0,0,0,0,0,0,0,0]]
Given the above grid, return 0.
Note: The length of each dimension in the given grid does not exceed 50.

  • idea
    bfs

  • code

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    class Solution {
    public:
        int maxAreaOfIsland(vector<vector<int>>& grid) {
            if (grid.empty()) {
                return 0;
            }
            int row = grid.size(), col = grid[0].size(), ans = 0;
            for (int r = 0; r < row; r++) {
                for (int c = 0; c < col; c++) {
                    if (grid[r][c] == 1) {
                        ans = max(ans, area(grid, r, c));
                    }
                }
            }
            return ans;
        }

    private:
        static int area(vector<vector<int>>& grid, int r, int c) {
            int row = grid.size(), col = grid[0].size(), area = 1;
            queue<pair<int, int>> myq;
            vector<int> dirs({-1, 0, 1, 0, -1});
            myq.push({r, c});
            grid[r][c] = 2;
            while (!myq.empty()) {
                int y = myq.front().first, x = myq.front().second;
                myq.pop();
                for (int i = 0; i < 4; i++) {
                    int new_y = y + dirs[i], new_x = x + dirs[i + 1];
                    if (new_y >=0 && new_y < row && new_x >= 0 && new_x < col && grid[new_y][new_x] == 1) {
                        grid[new_y][new_x] = 2;
                        area++;
                        myq.push({new_y, new_x});
                    }
                }
            }
            return area;
        }
    };

286. Walls and Gates

You are given a m x n 2D grid initialized with these three possible values.

-1 - A wall or an obstacle.
0 - A gate.
INF - Infinity means an empty room. We use the value 231 - 1 = 2147483647 to represent INF as you may assume that the distance to a gate is less than 2147483647.
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.

Example:

Given the 2D grid:

1
2
3
4
5
6
7
8
9
10
INF  -1  0  INF
INF INF INF  -1
INF  -1 INF  -1
  0  -1 INF INF
After running your function, the 2D grid should be:

  3  -1   0   1
  2   2   1  -1
  1  -1   2  -1
  0  -1   3   4

  • idea
    bfs

  • code:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    class Solution(object):
        def wallsAndGates(self, rooms):
            """
            :type rooms: List[List[int]]
            :rtype: void Do not return anything, modify rooms in-place instead.
            """
            self.inf = 2**31 - 1
            if not rooms or len(rooms) == 0:
                return None
            
            que = []
            visited = {}
            for i in range(len(rooms)):
                for j in range(len(rooms[0])):
                    if rooms[i][j] == 0:
                        que.append((i, j))
                        visited[(i, j)] = True
        
            while que:
                h = que.pop(0)
                i, j = h[0], h[1]
                c = rooms[i][j]
                for dx, dy in zip([0, 1, 0, -1], [1, 0, -1, 0]):
                    ii, jj = i + dx, j + dy
                    if ii < 0 or ii >= len(rooms) or jj < 0 or jj >= len(rooms[0]) or visited.get((ii, jj)) or rooms[ii][jj] == -1:
                        continue
                    que.append((ii, jj))
                    rooms[ii][jj] = c + 1
                    visited[(i, j)] = True

Posted on | In 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct Node {
	int val;
	struct node* left;  //左孩子
	struct node* right;  //右孩子
}

// pre-order: root, left, right
Node* p = root;
std::stack<Node*> s;
while (!s.empty() || p) {
    if (p) {
    	//边遍历边打印，并存入栈中，以后需要借助这些根节点(不要怀疑这种说法哦)进入右子树
        cout << p->val << endl;
        s.push(p);
        p = p->left;
    } else {
        //当p为空时，说明根和左子树都遍历完了，该进入右子树了
        p = s.top();
        s.pop();
        p = p->right;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// in-order: left, root, right
Node* p = root;
std::stack<Node*> s;
while (!s.empty() || p) {
    if (p) { 	
        //代码段(i)一直遍历到左子树最下边，边遍历边保存根节点到栈中
        s.push(p);
        p = p->left;
    } else { 
        //当p为空时，说明已经到达左子树最下边，这时需要出栈了
        p = s.top();
        s.pop();
        cout << s->val << endl;
        //进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)
        p =  p->right;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// post-order
/*
 *   后序遍历递归定义：先左子树，后右子树，再根节点。后序遍历的难点在于：
 *   需要判断上次访问的节点是位于左子树，还是右子树。若是位于左子树，则需
 *   跳过根节点，先进入右子树，再回头访问根节点；若是位于右子树，则直接访
 *   问根节点。直接看代码，代码中有详细的注释。
 *
 */
Node* cur = root;
Node* pre;
std::stack<Node*> s;

//先把cur移动到左子树最下边
while (cur) {
    s.push(cur);
    cur = cur->left;
}

while (!s.empty()) {
    //走到这里，cur都是空，并已经遍历到左子树底端(看成扩充二叉树，则空，亦是某棵树的左孩子)
    cur = s.top();
    s.pop();

    //一个根节点被访问的前提是：无右子树或右子树已被访问过
    if (s->right == NULL || s->right = pre) {
        cout << s->val << endl;
        //修改最近被访问的节点
        pre = cur;
    } else { 
        // 访问右子树，先把根节点再入栈
        s.push(cur); 

        //进入右子树，且可肯定右子树一定不为空
        cur = s->right;
        while (cur) {
            s.push(cur);
            cur = cur->left;
        }
    }
}

Posted on | In

再去加州，再次面试，这个时候保持的心态是佛系了，尽人事就好。所幸，我认识了这么多好的朋友，这么多好兄弟，他们也在自己的路上，面对不同的挑战。只要一个人不孤独就好。果然写点东西心里会舒服点。好好准备。活好自己就行了，别人也不会管你的。多运动，好好做好手头上面的事情。我心于业（My heart is in the work）。

Posted on | In

经历了三天的TOC，拿到了一些面试吧。回头看下，感觉自动驾驶这个领域的bar真的是好高好高。《棋魂》里面说过一句话：你不害怕，是因为你看不到我的剑锋，你害怕了，是因为你看到了。田渊栋大大说的好：做研究，你不仅先要看到剑锋，还要有迎难而上的勇气，无数次被打趴下来后，再无数次从绝望中找到一丝希望，然后费九牛二虎之力，从密密麻麻的错误里面，一点一点地挖出哪里米粒般的宝石来。
我只开始以为自己准备了暑假，找了个搞自动驾驶的老师，做了一点点项目，还有刷了刷题，以及积累了一些面试经验后，能很快看到结果。
现在发现，我才刚刚开始，我需要做好打持久战的准备，进入一个新的领域，然后不断的去面试。以及，以战养战。我能预期，自己在这个过程中，应该是不断的面挂，但是自己在这个过程里面，需要有一个清晰的思路，从面试里面发现自己的不足，及时补上。
所以，我现在还是继续之前的一些方案，白天research好好做项目，晚上刷题，投简历，周末一天刷题，一天查漏补缺，以及对research进行填补。然后，关于面试的话，最想去的公司，可以放一放，不要面试太密集，不好消化，这样子只会浪费机会，把backup先面了，练练手，同时注意和自己项目的balance。
然后，关于补缺知识，先是以自己项目里面涉及的为主，然后在博客这里面慢慢去整理。
再是，关于刷题，其实leetcode200多道题，lintcode135道，自己刷题的数量已经可以，但是自己现在其实需要的更多是质量而不是数量了，短时间自己在边research schedule两个projects，一边找工作也没有可能一下子在刷几百道，性价比更高的是，自己开始重新做一遍自己做的题，以及好好整理总结。博客这里的，leetcode section也需要抽点时间好好refine一下了。

Posted on | In

SVD

$X_{k \times } = U S V^T$

  • $X = [x_1, x_2, …, x_m] \in R^{N \times m}$
  • U is a m x m matrix, where $U^TU = I$
  • V is a n x n matrix, where $V^TV = I$
  • S is a m x n matrix, where.

Example

SVD fit 3D point

PCA

Posted on | In

Paper

  • Gaze Estimation from Multimodal Kinect Data
  • author
    Kenneth Alberto Funes Mora and Jean-Marc Odobez
    Idiap Research Institute, CH-1920, Martigny, Switzerland E ́colePolytechniqueFe ́de ́raldeLausanne,CH-1015,Lausanne,Switzerland
  • link: https://ieeexplore.ieee.org/document/6239182/

Gaze Estimation

  • tracking where the people look at.

Summary

  • exploit the depth sensor to perform an accurate tracking of a 3D mesh model and robustly estimate a person head pose
  • compute a person’s eye-in-head gaze direction via usage of the image modality.

Related Works

Pipeline

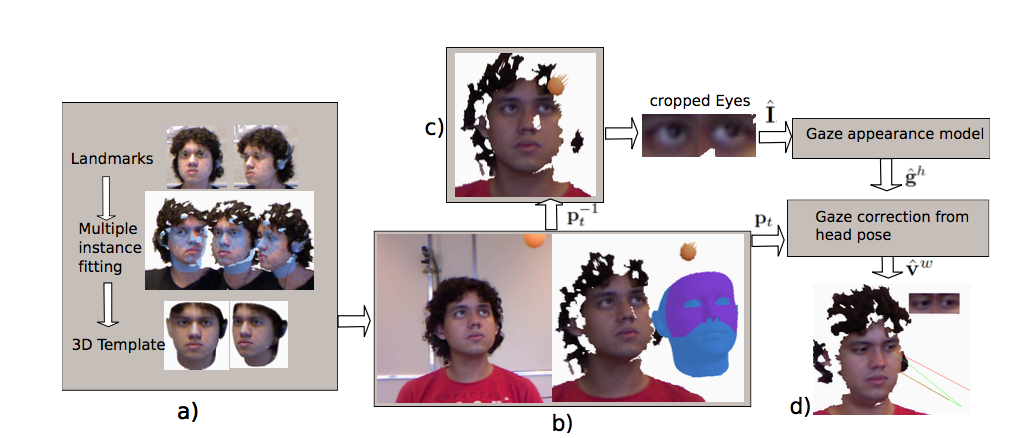
  • a) Offline step.
    From multiple 3D face instances the 3DMM is fit to obtain a person specific 3D model.
  • b)-d) Online steps.
    • b) The person model is registered at each instant to multimodal data to retrieve the head pose. In the figure, the model is rendered with a horizontal spacing for visualization. The region used for tracking is rendered in purple.
    • c) Head stabilization computed from the inverse head pose parameters and 3D mesh, creating a frontal pose face image. Further steps show the gaze estimation in the head coordinate system. The final gaze vector is corrected according to the estimated head pose.
    • d) Obtained gaze vectors (in red our estimation and in green the ground truth).

3D Morphable Model/Basel Face Model

The faces are parameterized as triangular meshes with m = 53490 vertices and shared topology.

  • vertices:
    • $(x_j, y_j, z_j)^T \in R^3$
    • $s = (x_1, y_1, z_1, …, x_m, y_m, z_m)^T$
  • colors:
    • $(r_j, g_j, b_j)^T \in [0, 1]^3$
    • $t = (r_1, g_1, b_1, …, r_m, g_m, b_m)^T$

BFM assumes independence between shape and texture, constructing two independent Linear Models, $M_s = (\mu_s, \sigma_s, U_s)$, $\mu_t, \sigma_t, U_t$

  • $s(\alpha) = \mu_s + U_s diag(\sigma_s)\alpha$
  • $t(\beta) = \mu_t + U_t diag(\sigma_t)\beta$

Pose Tracking/ICP (Iterative Closest Points)

  • Given: two corresponding point sets,
    • $x = {x_1, …, x_n}$, $P = {p_1, …, p_n}$
  • Wanted: translation t and rotation R thatminimizes the sum of the squared error:
    • $E(R, t) = \frac{1}{N_p}\sum_{i=1}^{N_p}(x_i - Rp_i -t)^2$
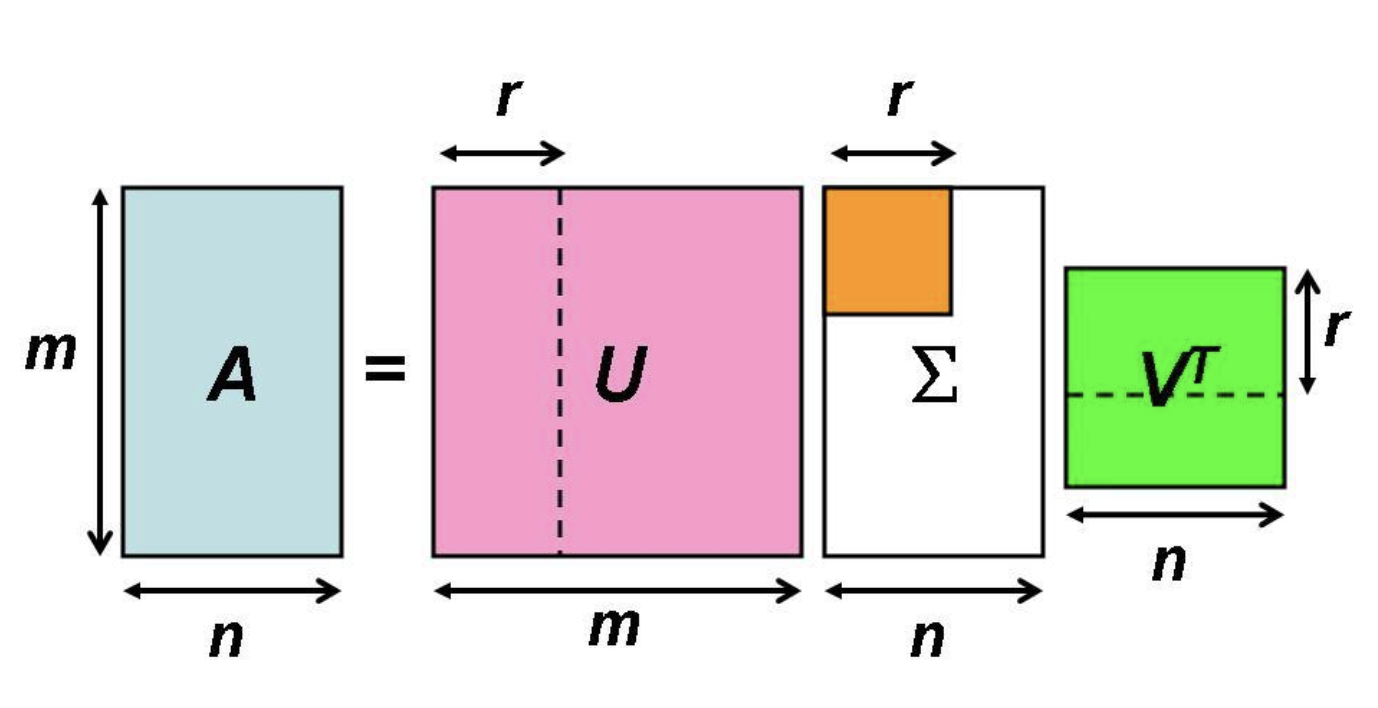
  • solution: SVD

Head stabilization

render the scene using the inverse rigid transformation of the head pose parameters. $p_t^{-1} = {R_t^T, -R_t^Tt_t}$

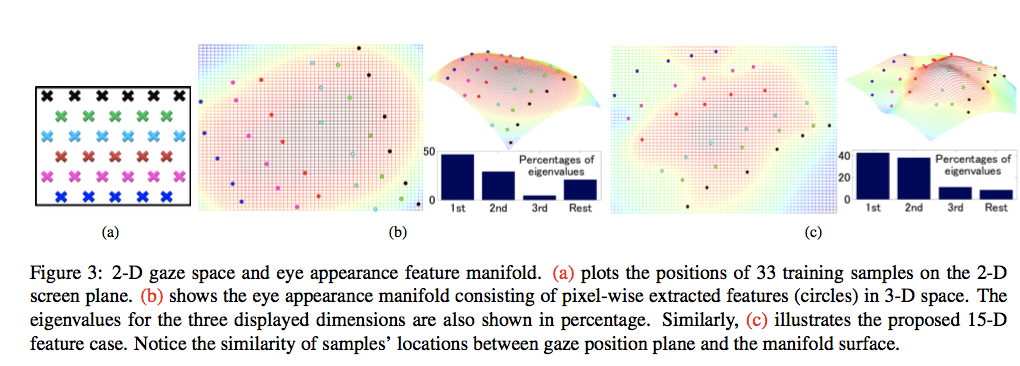
Eye-in-Head Gaze estimation/Adaptive Linear Regression

  • Key idea:

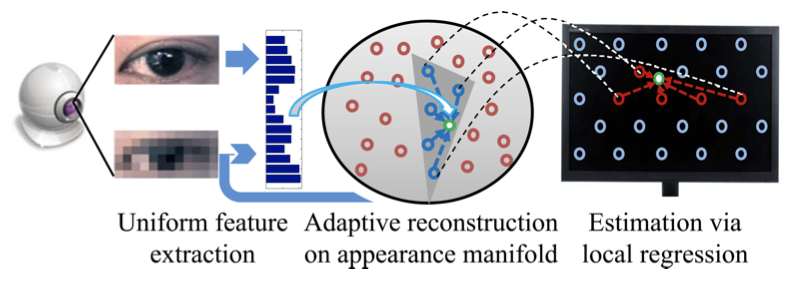
    • is to adaptively find the subset of training samples where the test sample is most linearly representable.

  • eye appearance feature extraction:

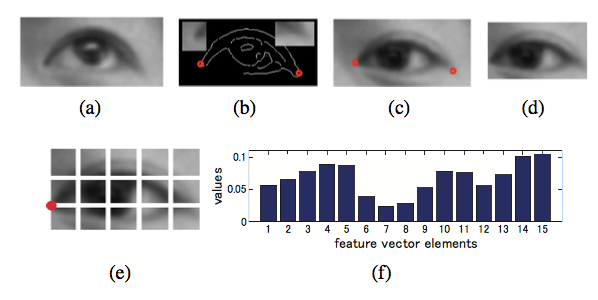
    • feature vector: $e_i = \frac{[s_1, s_2, …, s_{r \times c}]^T}{\sum_j S_j}$
    • $E = [e1,e2,··· ,en] ∈ R^{m×n}, X = [x1, x2, · · · , xn] ∈ R^{2×n}$
    • $AE = X$

Posted on | In

CRF in deeplab

Traditionally, conditional random fields (CRFs) have been employed to smooth noisy segmentation maps.
Typically these models couple neighboring nodes, favoring same-label assignments to spatially proximal pixels. Qualitatively, the primary function of these short-range CRFs is to clean up the spurious predictions of weak classi- fiers built on top of local hand-engineered features.

The score maps are typically quite smooth and produce homogeneous classification results. In this regime, using short-range CRFs can be detrimental, as our goal should be to recover detailed local structure rather than further smooth it.