eyewair

Posted on | In

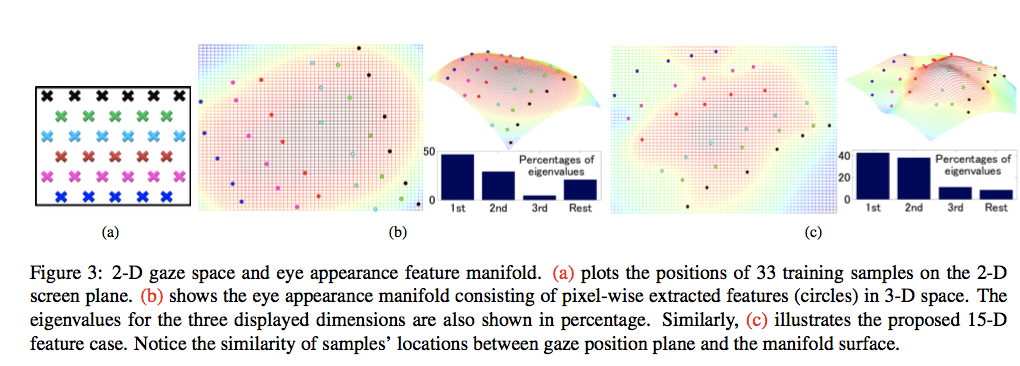
Paper

  • Gaze Estimation from Multimodal Kinect Data
  • author
    Kenneth Alberto Funes Mora and Jean-Marc Odobez
    Idiap Research Institute, CH-1920, Martigny, Switzerland E ́colePolytechniqueFe ́de ́raldeLausanne,CH-1015,Lausanne,Switzerland
  • link: https://ieeexplore.ieee.org/document/6239182/

Gaze Estimation

  • tracking where the people look at.

Summary

  • exploit the depth sensor to perform an accurate tracking of a 3D mesh model and robustly estimate a person head pose
  • compute a person’s eye-in-head gaze direction via usage of the image modality.

Related Works

Pipeline

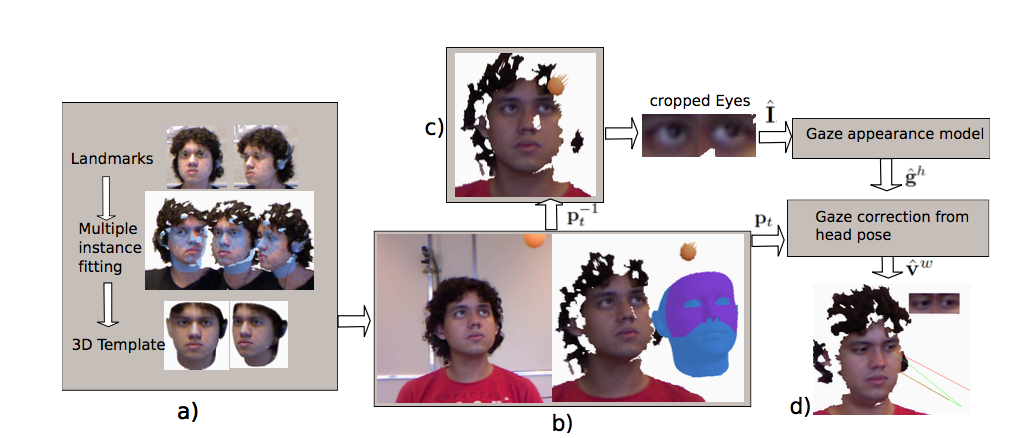
  • a) Offline step.
    From multiple 3D face instances the 3DMM is fit to obtain a person specific 3D model.
  • b)-d) Online steps.
    • b) The person model is registered at each instant to multimodal data to retrieve the head pose. In the figure, the model is rendered with a horizontal spacing for visualization. The region used for tracking is rendered in purple.
    • c) Head stabilization computed from the inverse head pose parameters and 3D mesh, creating a frontal pose face image. Further steps show the gaze estimation in the head coordinate system. The final gaze vector is corrected according to the estimated head pose.
    • d) Obtained gaze vectors (in red our estimation and in green the ground truth).

3D Morphable Model/Basel Face Model

The faces are parameterized as triangular meshes with m = 53490 vertices and shared topology.

  • vertices:
    • $(x_j, y_j, z_j)^T \in R^3$
    • $s = (x_1, y_1, z_1, …, x_m, y_m, z_m)^T$
  • colors:
    • $(r_j, g_j, b_j)^T \in [0, 1]^3$
    • $t = (r_1, g_1, b_1, …, r_m, g_m, b_m)^T$

BFM assumes independence between shape and texture, constructing two independent Linear Models, $M_s = (\mu_s, \sigma_s, U_s)$, $\mu_t, \sigma_t, U_t$

  • $s(\alpha) = \mu_s + U_s diag(\sigma_s)\alpha$
  • $t(\beta) = \mu_t + U_t diag(\sigma_t)\beta$

Pose Tracking/ICP (Iterative Closest Points)

  • Given: two corresponding point sets,
    • $x = {x_1, …, x_n}$, $P = {p_1, …, p_n}$
  • Wanted: translation t and rotation R thatminimizes the sum of the squared error:
    • $E(R, t) = \frac{1}{N_p}\sum_{i=1}^{N_p}(x_i - Rp_i -t)^2$
  • solution: SVD

Head stabilization

render the scene using the inverse rigid transformation of the head pose parameters. $p_t^{-1} = {R_t^T, -R_t^Tt_t}$

Eye-in-Head Gaze estimation/Adaptive Linear Regression

  • Key idea:

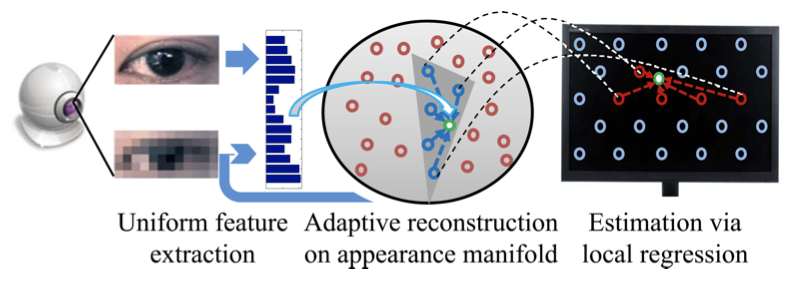
    • is to adaptively find the subset of training samples where the test sample is most linearly representable.

  • eye appearance feature extraction:

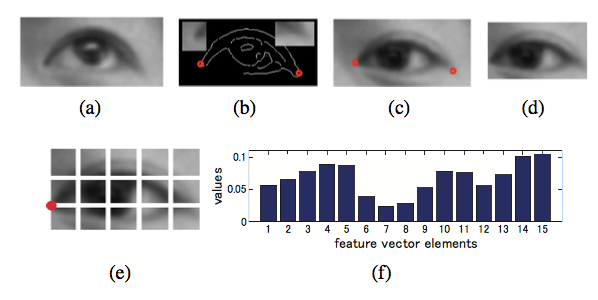
    • feature vector: $e_i = \frac{[s_1, s_2, …, s_{r \times c}]^T}{\sum_j S_j}$
    • $E = [e1,e2,··· ,en] ∈ R^{m×n}, X = [x1, x2, · · · , xn] ∈ R^{2×n}$
    • $AE = X$