This blog refers to this paper
Abstract
We propose a method for semi-supervised semantic segmentation using the adversarial network. While most existing discriminators are trained to classify input images as real or fake on the image level, we design a discriminator in a fully convolutional manner to differentiate the predicted probability maps from the ground truth segmentation distribution with the consideration of the spatial resolution. We show that the proposed discriminator can be used to improve the performance on semantic segmentation by coupling the adversarial loss with the standard cross entropy loss on the segmentation network. In addition, the fully convolutional discriminator enables the semi-supervised learning through discovering the trustworthy regions in prediction results of unlabeled images, providing additional supervisory signals. In contrast to existing methods that utilize weakly-labeled images, our method leverages unlabeled images without any annotation to enhance the segmentation model. Experimental results on both the PASCAL VOC 2012 dataset and the Cityscapes dataset demonstrate the effectiveness of our algorithm.
Architecture and training pipeline
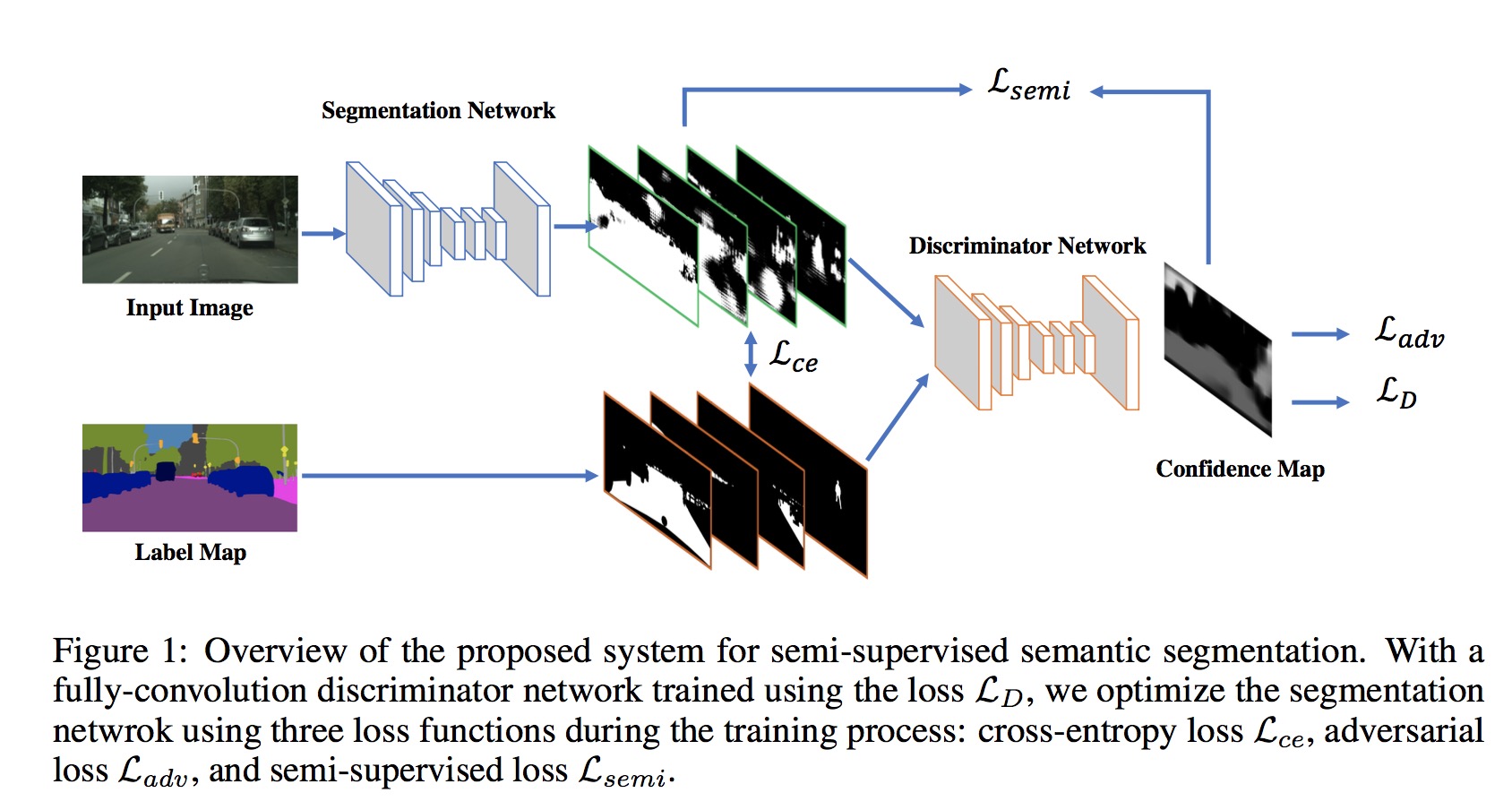
The authors firstly train the segmentation network with cross-entropy loss and adversarial loss and the discriminitor network with cross-entropy loss in labeled data. Then, the training of unlabeled data is performed under the semi-cross-entropy loss with the self-taught ground truth from the trained discriminitor network and threshold settings.
Discriminator network training
$L_D = -\sum_{h, w} (1-y_n)log(1-D(S(X_n)^{h, w})) + y_n D(Y_n)^{h, w}$
$X_n$ is the input image, whose size is H x W x 3. S() is the segmentation network, whose input is $X_n$ and output is H x W x C probability maps. And D() is discriminator network, which takes H x W x C probability maps and predict the probabilities for each pix from segmentaiton network or groundtruth. Thus, the cross-entropy loss is binary cross-entropy, where $y_n = 0$ if the sample is drawn from segmentation network and $y_n = 1$ if the sample is from ground truth label.
Segmentation network training
$L_{seg} = L_{ce} + \lambda_{adv} L_{adv} + \lambda_{semi} L_{semi}$
where $L_{seg}, L_{ce}$ and $L_{adv}$ denote multi-class cross-entropy loss, adversarial loss and semi-supervised loss, respectively, $\lambda_{adv}$ and $\lambda_{semi}$ are two constants for balancing the multi-task training.
Training with labeled data
$L_{ce} = -\sum_{h, w} Y_n^{(h, w, c)}log(S(X_n)^{(h, w, c)})$
, where $Y_n$ is one-hot encoded ground truth, and $S(X_n)$ is the prediction probability maps.
$L_{adv} = -\sum_{h, w} log(D(S(X_n))^{h, w})$
with this adversarial loss, we seek to train the segmentation network to fool the discriminator by maximizing the probability of the segmentation prediction being considered as the ground truth distribution.
In fact, you can regard $D(S(X_n))$ as $D(S(X_n)) = P(y_n=1|S(X_n))$, which means the probability where sample are drawn from segmentation network but the discriminator assume it’s from ground-truth.
Training with un-labeled data
$L_{semi} = -\sum_{h,w}\sum_{c \in C}I(D(S(X_n)^{h,w} > T_{semi}) \hat{Y}_n^{(h,w,c)}log(S(X_n)_{(h,w,c)})$
where, $\hat{Y_n} = argmax(S(X_n))$ the masked segmentation prediction, $T_{semi}$ is threshold to control the sensitivity of the self-taught process, since there’s no ground-truth for $L_{ce}$.