介绍
这篇论文是首次将domain adaptation应用到self-driving的semantic segmentation里面,和FCN在segmentation里面是一样算是开篇之作。
abstract
Fully convolutional models for dense prediction have proven successful for a wide range of visual tasks. Such models perform well in a supervised setting, but performance can be surprisingly poor under domain shifts that appear mild to a human observer. For example, training on one city and testing on another in a different geographic region and/or weather condition may result in significantly degraded performance due to pixel-level distribution shift. In this paper, we introduce the first domain adaptive semantic segmentation method, proposing an unsupervised adversarial approach to pixel prediction problems. Our method consists of both global and category specific adaptation techniques. Global domain alignment is performed using a novel semantic segmentation network with fully convolutional domain adversarial learning. This initially adapted space then enables category specific adaptation through a generalization of constrained weak learning, with explicit transfer of the spatial layout from the source to the target domains. Our approach outperforms baselines across different settings on multiple large-scale datasets, including adapting across various real city environments, different synthetic sub-domains, from simulated to real environments, and on a novel large-scale dash-cam dataset.
摘要里面最重要的应该是这句话了,global and category specific adaptation techniques,后面会详细介绍。
Fully Convolutional Adaptation Models
source domain and target domain
既然是涉及transfer,这里就要有source domain (源域),$S$,这里就有图片空间$I_S$和对应的标注空间$L_S$。我们训练得到$\phi_S(I_S)$。然后我们的目标是,学习一个语义分割的模型,它适用于没有被标注的目标域(target domain)$T$,有图片空间$I_T$。我们用$\phi_T()$来表示这个模型。
domain shifts
- global changes,会导致特征空间的边缘概率分布的不同
这个常常是会出现在两个不用的领域里面,两个领域的越是不同,shift会越大,比如:模拟的数据和实际数据。 - category specific parameter changes
不同类在两个不同的领域里面会有不同的偏差,比如:车和标志在不同领域里面的做迁移的时候,分布的改变会不同。
loss function
我需要假设,源域和目标域有同样的标注空间,以及源域训练得到的模型比目标域有更好的效果。
然后基于上面的shifts,我们需要两个loss function:
- $L_da(I_S, I_T)$:
这个和global的distribution distance相关 - $L_mi(I_T, P_{L_S})$:
这个和category specific parameters有关,其中,$P_{L_S}$表示的是从源域迁移过来的标注空间的概率分布
此外我们还需要一个loss function: - $L_seg(I_S, I_T)$:
这个是在源域上面的标准的监督分割的一个目标函数,就是正常的我们在source data上面训练的一个loss function而已。
所以最后的loss function:
$L(I_S, I_T, P_{L_S}) = L_{da}(I_S, I_T) + L_{mi}(I_T, P_{L_S}) + L_{seg}(I_S, I_T)$
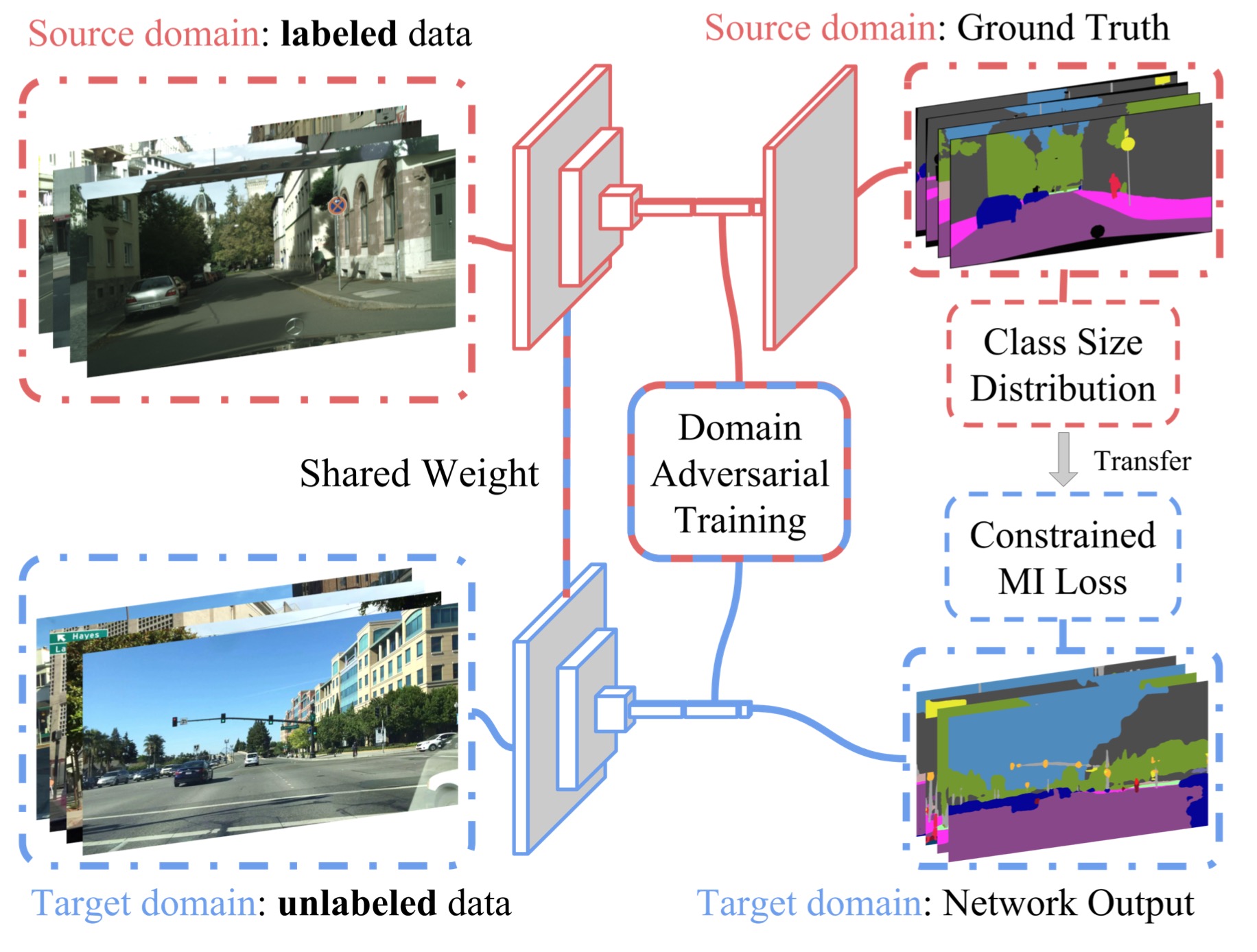
这张图很好的呈现了整个过程的pipeline,$L_{seg}(I_S, I_T)$是在source domain data上面训练的;fully-convolutional domain adversarial training则是用来降低,源和目标域概率分布不同的距离;我们又通过constrained pixel-wise multiple instance learning objective在目标域上面的数据训练,来完成category specific的更新。
Global Domain Alignment
这里我们详细阐述$L_{da}(I_S, I_T)$,然后重申一遍,我们需要减小源域和目标的域偏移,然后我们采用的是domain adversarial (域的对抗学习)的方法。
- 我们需要回答的第一个问题是:在这个密集的预测框架里面,需要由什么来组成一个实例?
回答是考虑最终一个表示层的每一个空间单元的自然接受域所对应的区域,作为独立的实例。换句话说,我们不在网络的最后一层,而是在有pixel prediction的前一层进行操作。
我们将这一层的结果用$\phi_{l-1}(\theta, I)$来表示,它对应的参数是$\theta$。 - 接下来我们来进一步拆解,我们的domain adversarial loss,它有交替的最小化目标组成。
- 一是在表示空间,我们想要最小化源域和目标域的距离:$d(\phi_{l-1}(\theta, I_S), \phi_{l-1}(\theta, I_T))$
- 二是我们需要通过训练区分源域和目标域实例的域判别器来估计这个距离,我们将判别器的参数设为$\theta_D$
我们需要让这个判别器来学习源域区域和目标域区域的不同,进而来使源域和目标域在表示空间上的距离最小。
- loss function and inverse domain loss function:
$L_D = - \sum_{I_S \in S}\sum_{h \in H}\sum_{w \in W}log(P_{\theta_D}(R_{hw}^S)) - \sum_{I_T \in T}\sum_{h \in H}\sum_{w \in W}log(1 - P_{\theta_D}(R_{hw}^T))$
$L_{Dinv} = - \sum_{I_S \in S}\sum_{h \in H}\sum_{w \in W}log(1 - P_{\theta_D}(R_{hw}^S)) - \sum_{I_T \in T}\sum_{h \in H}\sum_{w \in W}log(P_{\theta_D}(R_{hw}^T)) $- $P_{\theta_D} = \sigma(\phi(\theta_D, x))$
- output layer l-1: $H \times W$ spatial units
- $R_{hw}^S = \phi_{l - 1}(\theta, I_S)_{hw}$ denote source representation of each unit
- $R_{hw}^T = \phi_{l - 1}(\theta, I_T)_{hw}$ denote target representation of each unit
然后有了这些定义,我们来交替优化这两个目标函数了:$\min_{\theta_D} L_D$,$\min_{\theta} \frac{1}{2}[L_D + L_{Dinv}]$ 前者是学习相关图片域里面最有可能的域分类器,